The Decagon and The Star Decagon

Proposition 40

The Regular shape with 24 sides, and all figures obtainable from it by repeated doubling of the number of sides, can be inscribed in the circle Geometrically.

But the knowledge of the side strays further into degrees still more distant from those considered earlier.

The same applies to the sides of its stars, which subtend 5, 7, or 1 1 twenty-fourths [of the circle].

This is proven as Proposition 37 above was from the 16-sided figure. The difference is that here the side of the star Dodecagon and half of it are first Binomials, so that the rectangle contained by the half [side] and the diameter, [the latter] being Expressible. This time does not yet come to be of a new species, because by 54, the side of the area is again a BinomiaV

But now this rectangle, subtracted from the Expressible [rectangle contained by] the complete [diameter] and the half Diameter, leaves a new species, of which no mention has so far been made, and of lower degree, because more composite.

This is produced by the square of the side of the figure with 24 angles.

This is all the more true for figures of this Class with more angles; such as figures with 48 angles, 96 angles and so on.

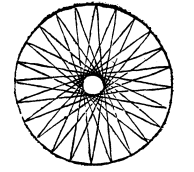
The chord subtended by five twenty-fourths of the circle is disclosed by bisection of the arc containing five twelfths: the square of the former [i.e. ii] subtracted from the square of the diameter, leaves the square of the chord subtended by 7 24ths^’-’’^: so the square of the side, or the chord subtended by 1 24th, in the same way forms the square of the chord subtended by eleven such parts.^’^^ So they all belong to a more distant degree.

Proposition 41

The side of the Decagon and that of the star decagon, or the chord subtended by three tenths of the circle,*^ have a Geometrical description through their angles, and can be inscribed in the circle; and they are knowable, separately as individuals indeed in the eighth Degree of knowledge, while combined [they are of] the fifth degree; and combined with the semidiameter they are of the fourth degree.

Let the Decagon be BCDEFGHIKL, and its star BEHLDGKCFIB. Therefore, since there are ten angles, the surface of the figure will be composed of ten triangles meeting at the center A, one of which [triangles] is FAG. So di­ viding up the sum of four right angles, which surrounds the point A, into the ten vertical angles of these triangles, each one comes to 4 tenths or 2 fifths of one right angle. But the sum of the three angles of this triangle is 10 fifths, that is 2 Right angles; therefore taking from this the vertical angle at A of two fifths, the remainder left for the two base angles is 8fifths: and since they [the base angles] are equal, each of them is of [size] 4 fifths. Thus each of the base angles is twice the angle at the vertex. The proof thatfollows hangs on this [result]. For if the angle AFG is divided into two equal parts by the line FO, using Euclid 1.9^^^; the angles AFO, OFG will be equal to one another, and each will be 2 fifths of the Right angle; thus each will be equal to the angle FAO. So by Euclid VI.3,^^^ the ratio of A F to FG will be equal to the ratio of AO to OG. Now because [angle] OFG is 2 fifths [of a right angle], and the angle OGF (namely AGF) was 4 fifths, therefore [angle] FOG will also be 4 fifths. So the angles at O and G being equal, the sides opposite them, FG, FO will also be equal. In the same way, in the triangle AOF also, since [angle] AFO is 2 fifths [of a right angle], as was angle FAO; therefore AO and FO (that is the side [of the decagon] FG) will be equal to one another. Now, the ratio of A F to FG is equal to the ratio of AO to OG, as already proved; therefore, also, the ratio of AG to its part, AO, is equal to the ratio of the latter to the remainder, OG. Thus the Leg^^^ AG is divided proportionately in the point So, by Euclid X///.5, if OA or OF, is produced to so that 01 is equal to the whole line AG, FI is also divided proportionately at O, and if the points A and I are joined, AIO will be a triangle congruent (congruum) with the initial triangle FAG, so that [the angle] OAI will be twice [the angle] FAO, and [angle] FAI will be 6 fifths [of a right angle].

Accordingly, if with center A, and compass opening AG, the circle FGI is drawn, FG will be the side of the decagon, the greater part ]produced when] the semidiameter is divided proportionately, and FI the side of the star, or the chord subtended by three tenths [of the circle], is the line composed of ]i.e. the sum of] FO and 01, [that is] the side of the decagon and the semidiameter.

On account of this, these sides, taken together with the semidiameter, can be accepted as belonging to the fourth degree, by XXVI above.

Since the line that is divided [in proportional section], AG, is Expressible in length, and the side of the decagon is the larger part [produced by the division]; and the side of the star is composed of [i.e. the sum of] the whole [line AG] and its greater part;

Accordingly, by XXVII above, the former [the side of the decagon] is an Apotome and the latter [the side of the star] is a Binomial, each of the fourth kind}^^ in this respect they belong to the eighth degree of knowledge, closely following the side of the Dodecagon and its star, and exactly on a level with the side of the Octagon and its star.

By XXIIX above, the remainder OG also, and also half of it, NG, is an Apotome of the first kind. But beware of supposing that AG is its greater term and AN its smaller one.

Finally, by the same XXVII above, the sides GF, or OF, and FI combined not with the semidiameter but with each other belong to the fifth degree of knowledge, because both the sum of their squares and their common Rectangle are Expressible.

So adding together the side of the Decagon and the side of its star gives a line expressible only in square, its square being equal to five fourths of the square of the semidiameter, which [i.e. this line] in the earlier figures from Prop. XXVII is [shown as] PX, composed of PA (equal to the line OA) and AX: between which there is the mean proportional GA which is expressible.

On the other hand, subtracting the side of the Decagon, OF, from the side of the star, FI, leaves the Expressible line 01, that is the semidiameter.

So this gives nothing new.