Measurements

Proposition 29

When a division in proportional section is made on any line that is a Mizon

Its square is equal to the rectangle with length compounded from a given expressible line and the line whose square is 5 fourths that of the given expressible line, and with breadth whose square is 5 fourths [of the same square];

Then the smaller part will be an Elasson: where Elasson is a term not of comparison but denoting quality: while the greater part will be another Mizon, [the term] again being understood qualitatively, whatever its Elements may be.

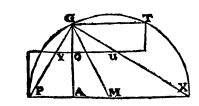
As before, let half of the proposed line expressible in length be GA, and half of that again be AM; so that in units such that the square of GA is 4 the square of AM is 1, and let GAM be a right angle, so in these units the square of MG will be 3.

Let MA be produced in both directions. With center M and radius MG let there be drawn a semicircular arc PGX.

So PX is twice the line GM;

Therefore, the square ofPX will also befive fourths of the square of the proposed line, twice the pro­ posed line GA. But the combined squares of PG and GX are equal to the square of PX, therefore they too are five fourths of the square of the proA. \M posed expressible line.

If you put PG and PX together to make one line, its square will consist of the two squares of PG and GX and two Rectangles contained by PG and GX, which are equal to two rectangles contained by GA and PX, that is one rectangle contained by the proposed line, double the line GA, and the line PX, two lines which are both expressible but are commensurable only in square: on which account this rectangle will be Medial, by Euclid X.22.

So since the square of the whole line PGX consists of the expressible square of PX, and a Medial rectangle, with the same breadth PX: which two, the square of PX X and the rectangle contained by twice the line GA and the line PX, are equal to the rectangle which is contained by PX, an expressible line, and the line which is the compound of PX and twice the line GA, [parts] which are commensurable only in square, of which parts the greater, PX, has a square greater than that of the smaller (twice the line GA) by an amount incommensurable with it [i£. PX] in length (for the square of PX is 5 in units such that the square of twice the line GA is 4, so the excess, 1, is the square of some line which is incommensurable with the line PX, because the ratio of 1 to 3 is not that of one square number to another) for which reasons the said line, constructed by compounding PX and twice GA, is a Binomial of the fourth kind: since, I say, the square of the whole line PGX is equal to such a rectangle contained by a fourth Binomial and an Expressible: therefore the whole line PGX will be Medial.

The Elements which compose it are the parts PG and GX.

For because PA is an Apotome and AX a Binomial: therefore they are Incommensurable with one another in length.

The ratio of PA to AX is the same as the ratio of the square of PG to the square of GX. Therefore PG and GX are incommensurable with one another in square and thus also simply incommensurable.

The sum of their squares is expressible, in fact equal to the square of PX*’^; and the rectangle contained by PG and GX is Medial. Therefore by X.39j^ the line constructed by compounding PG and GX is a Mizon: and by X.76, subtracting PG from GX, the remainder is an Elasson [Minor].

Anyway, the whole line PGX is divided in proportional section at G. For the ratio of PA to AG is equal to the ratio of PG to XG.

But PA is [equal to] OA the greater part formed by dividing the line GA in proportional section, because the square of MP is 5 times the square of the line MA and the Apotome AP is equal to AO by Euclid

Therefore PG is also the greater part formed by dividing the line G in proportional section; and by X///.5,’** adding PG, the greater part, to GX, the whole line, we obtain a new whole line PGX which is divided in proportional section at the point G; so now PG is the smaller part of this compound line, and GX its greater part.

Thus PGX, which is a Mizon, is divided at the same point G both into its Elements, from which it is characterized as a Mizon, and also at the same time into parts in divine proportion.

These parts produced by proportional section are at the same time both an Elasson and a Mizon.’^"^ For because AP is a fourth Apotome, therefore [the rectangle] contained by AP, an Apotome, and PX, an Expressible line, has an area equal to that of a square whose side is an Elasson, by Euclid X and because AX is a fourth Binomial, therefore [the rectangle] contained by this line and PX, an Expressible line, has an area equal to that of a square whose side is a mizon: but the squares of PG and GX are equal to the rectangles APX, AXP^^ each to each, therefore PG is an Elasson and GX a Mizon.

So here we have agreement between the names of the qualities and the names of the proportions. For PG is called the smaller part {minor), with respect to the whole line PGX divided in proportional section at G; and it is also called a “minor” line or “minor” Element of the whole line PGX, as this is, qualitatively, a Mizon..

Finally, in Greek it is called, qualitatively, an Elasson (which corresponds to the Latin “minor”), this with respect to the other two lines, not shown here, from which it is constructed by their being subtracted one from another.

In the same way GX is firstly called the greater part {major) of the whole line PGX divided in proportional section; second it is called the “‘major’” line or Element of the whole line PGX, as this is, quali­ tatively, a Mizon in its own right, as also is the whole line PGX in its own right: but the lines which are compounded to construct the Mizon line GX are not shown here.

I believe it was on account of this agreement between division in proportional section and the division of a Mizon into its Elements that these qualitative Terms {Nomina) Mizon and Elasson came to be applied to these kinds [of line].

However, here we should take great care not to lose sight of the distinctions between things; proportional section is an absolute proportion, not tied to one particular line, the first to be mentioned, which proposed line is said to be Expressible’®: now the species.

Mizon and Elasson are conceived as indicating definite degrees of departure from the first proposed Expressible line.

So the division in divine proportion proceeds indefinitely; but the property of Mizon and Elasson does not follow it.

In the former (the course of repeated divisions) the part which was a greater part {major) becomes, at the next division, a smaller one {minor)’, in the latter, a line which was qualitatively an Elasson, never in any respect becomes a Mizon,®’ nor a Mizon an Elasson.

Thus if the Mizon GX is again divided in proportional section, its greater part will be equal to the line PG, and will thus qualitatively remain an Elasson; nor can it possibly become qualitatively a Mizon, as it can quantitatively become the greater part {major) [in the course of further division]: as long, that is, as GA is proposed as Expressible.

Do you wish to know why, if PGX is qualitatively a Mizon, and GX is also qualitatively a Mizon, then the greater Element of the line GX cannot also be a Mizon in the same way that the greater Element of the Mizon PGX, namely GX, was itself a Mizon?

The answer is that although both the lines PGX and GX are Mizons, the result is different in the former case from what it is in the latter.

For in the square of PGX we have the whole square of PX and the whole rectangle con­ tained by twice GA and the line P.

But in the square of GX, what is involved is [indeed] the square of PX but only half of it, namely the part that is contained by MX and XP, whereas of the rectangle contained by twice GA and the line P, we have only one quarter, namely that contained by AM and PX.

So in the latter case the proportion of Medial to Expressible is different from what it was in the former.

Our proposition strives to show that there is agreement between the quantitative results of division in divine proportion and the qualitative description of the parts only if the parts are those formed by the first division of the line PGX, depending on its particular proportion between Medial and Expressible [areas]; the proposition does not hold for further divisions.

Note the following contribution to the closeness of the analogy; that just as GX, a Mizon formed by division in divine proportion, makes another greater Mizon, namely PGX, by the addition of PG, which is the greater part obtained by dividing the line GX in divine proportion: so, on the other hand, PG an Elasson of this kind, formed by division in divine proportion, gives PY a smaller Elasson than itself, namely the greater part formed by division of the line PG, or GV, the smaller part formed by division of the line GX: so just as the greatest line, PGX, when divided in divine proportion, decomposes into the Mizon XG and the Elasson GP, so the second Mizon, GX, would decompose into two Elassons XV and VG, which are equal to GP and PY: and so two Elassons would be compounded to form one Mizon; while a Mizon and an Elasson make another Greater Mizon.