The Lorentz Transformation

Sections 8-10 show that the apparent incompatibility of the law of propagation of light with the principle of relativity (Section 7) arises from two unjustifiable hypotheses from classical mechanics:

1. The time-interval (time) between two events is independent of the body of reference

2. The space-interval (distance) between two points of a rigid body is independent of the body of reference

If we drop those two, then the dilemma of Section 7 disappears, because the addition of velocities (Section 6) becomes invalid*. This then makes the law of the propagation of light in vacuum compatible with the principle of relativity.

How can we modify Section 6 [addition of velocities] to unify space and time

Referring to my example of an event viewed from a moving train and an embankment= How should we think of the place and time of individual events relative to both reference-bodies [train and embankment], so that light has the velocity c relative to the embankment and to the train?

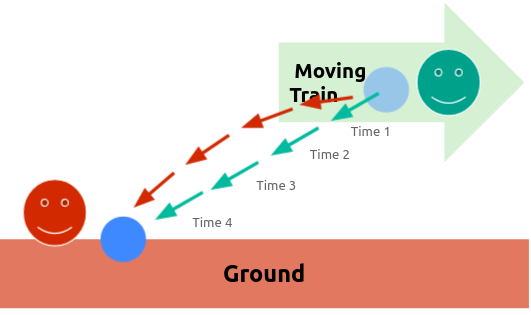
This is answered by a perfectly definite transformation law for the space-time magnitudes of an event when changing over from one viewpoint to another. The horizontal embankment is a viewpoint supplemented horizontally and vertically through a framework of rods as mentioned in Section 2. In this way, an event anywhere can be localised through such rods.

The train travelling with velocity v continues across the whole of space. Every event, no matter how far off it may be, could also be localised from the viewpoint of the train.

We can ignore the continual interference of these two viewpoints with each other arising from the impenetrability of solid bodies. In every such framework, we imagine a coordinate system of 3 surfaces perpendicular to each other.

• non-moving K is the embankment
• moving K' is the train.

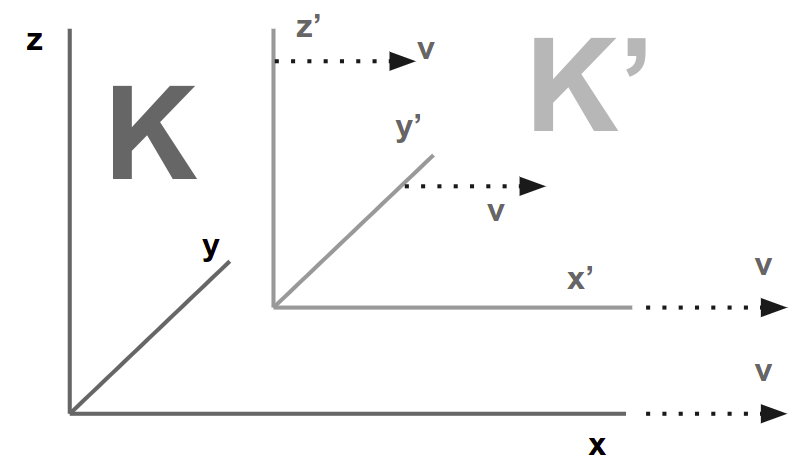
Relative to the non-moving K, an event would be:

• fixed in space with respect to non-moving K by the three perpendiculars x, y, z showing its coordinates
• fixed in time by a time-value t

Relative to moving K', the same event would be:

• fixed in space and time by corresponding values x', y', z', t'. These are different from x, y, z, t.

What are the values x', y', z', t' of an event with respect to the moving K' when the magnitudes x, y, z, t of the same event with respect to the non-moving K are given?

Lorentz Transformation

The relations must be so chosen that the law of the transmission of light in a vacuum is satisfied for lightrays with respect to K and K'. This is solved by equations known as the “Lorentz transformation.*”:

x' = (x - vt) / √(1-(v2/c2))

y' = y

z' = z

t' = (t-(v/c2))x) / √(1-v2/c2

Galileo Transformation

If we used instead the Classical mechanics [Section 9?] wherein space and time were absolute, then the equations would be:

x' = x − vt
y' = y
z' = z
t' = t

These are called the “Galilei transformation.” These can be obtained from the Lorentz transformation by substituting an infinitely large value for the velocity of light c in the Lorentz transformation. Thus, the law of the transmission of light in vacuum is satisfied both for the non-moving K and the moving K'.

A light signal is sent along the positive x-axis. It advances accordaning with the equation (with the velocity c)=

x = ct

According to the equations of the Lorentz transformation, this simple relation between x and t involves a relation between x' and t'. If we substitute for x the value ct in the 1st and 4th equations of the Lorentz transformation, we obtain=

x' = ( c − v ) t / √(1-(v2/c2)

t' = ( 1 − (v/c) ) t / √ (1 − (v2/c2)

from which, by division, the expression follows:

x' = ct'

If referred to the system K', the speed of light takes place according to this equation. We thus see that the velocity of transmission relative to the moving K' is also equal to c. The same result is obtained for rays of light advancing in any other direction.