Space And Time In Classical Mechanics

by Albert Einstein Icon

3 minutes • 427 words

The purpose of mechanics is to describe how bodies change their position in space with time.

What does “position” and “space” mean?

I stand at the window of a railway carriage which is travelling uniformly.

I drop a stone on the embankment, without throwing it.
Disregarding air resistance, I see the stone descend in a straight line.
A pedestrian on the footpath sees this and notices that the stone falls to earth in a parabolic curve.

Do the “positions” traversed by the stone lie on a straight line or on a parabola?

What does motion “in space” mean?

We should entirely shun the vague word “space”.

We replace it with “motion relative to a body of reference.”
We then replace this “body of reference” with “system of coordinates.” This will allow mathematical descriptions.

In this way:

relative to a system of coordinates rigidly attached to the carriage, the stone travels at a straight line
relative to a system of coordinates rigidly attached to the ground (embankment), the stone travels in a parabola

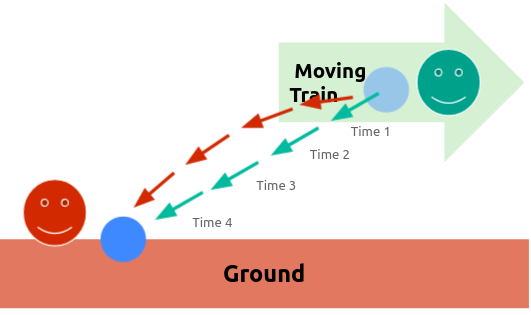
Moving Train Graphic — Einstein gives total importance to external movement. The problem with this is that such movement can be observed in infinite perspectives. If you extend this logic, this leads to field equations, using Galilean coordinates, that have no solution because they are inherently arbitrary. Moreover, the external-movement paradigm requires an external standard measure. For this, Einstein uses the speed of light. This is problematic because light only works for visible things, but the universe is mostly invisible. It also leads to his defintion of time as simultaniety, which is circular reasoning as he explains himself in Section 8. Instead of taking the perspective of the train and the ground, Superphysics takes the perspective of the stone. In Superphysics, the universal measure is ‘idea’, through the force-carrier called ’thought’. This allows the entire universe to be known, as long as our minds have the idea for it

This shows that there is no such thing as an independently existing trajectory. Instead all trajectories are relative to a viewpoint.

A complete description of a body’s motion must specify how that body changes its position with time. For every point on the trajectory, the time of the body must be stated. Such time-values are then the magnitudes (results of measurements) capable of observation.

Under Classical mecahnics, we imagine two identical clocks.

One is held by an observer in the railway-carriage window
The other is with an observer on the footpath

Each of the observers determines the position of the stone from his perspective at each tick of his clock.