Proposition 52, Theorem 40

Assume that:

• a solid sphere in an uniform and infinite fluid revolves around an axis given in position with a uniform motion
• the fluid is forced around by only this impulse of the sphere
• every part of the fluid perseveres uniformly in its motion.

The periodic times of the parts of the fluid are as the squares of their distances from the sphere’s centre.

Case 1:

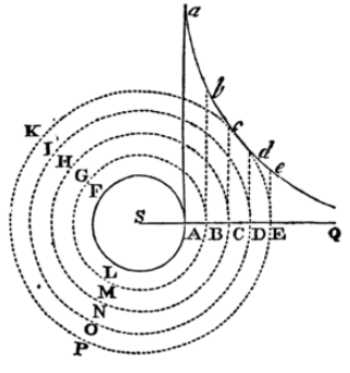
Let AFL be a sphere turning uniformly around the axis S.

The concentric circles BGM, CHN, DIO, EKP, etc., divide the fluid into innumerable concentric orbs of the same thickness.

Those orbs are solid.

The fluid is homogeneous.

The impressions which the contiguous orbs make one upon another will be the same as their

(by the supposition) as their

translations from one another, and the contiguous superfaces on which the impressions are made.

If the impression on any orb be greater or less on its concave than on its convex side, the more forcible impression will prevail. It will either accelerate or retard the orb’s velocity, according as it is directed with a conspiring or contrary motion to that of the orb.

Therefore the impressions made on both sides of the orb should be equal and have contrary directions so that every orb may persevere uniformly in its motion.

The impressions are as the contiguous superfaces just as their translations are from one another.

Therefore, the translations will be inversely as the surfaces – they are inversely as the squares of the distances of the surfaces from the centre.

But the differences of the angular motions around the axis are as those translations applied to the distances, or as the translations directly and the distances inversely. This is done by compounding those ratios, as the cubes of the distances inversely.

Therefore, assume that on the several parts of the infinite right line SABCDEQ there are the perpendiculars Aa, Bb, Cc, Dd, Ee, etc.

• These are reciprocally proportional to the cubes of SA, SB, SO, SD. SE, etc.,

Then the sums of the differences or the whole angular motions will be as the corresponding sums of the lines Aa, Bb, Cc, Dd, Ee, etc.

This assumes that, in order to constitute an uniformly fluid medium:

• the number of the orbs are increased
• the thickness of those orbs are reduced infinitely

The hyperbolic areas AaQ, BbQ, CcQ, DdQ., EeQ, etc. would be analogous to the sums.

The periodic times being reciprocally proportional to the angular motions, will be also reciprocally proportional to those areas.

Therefore the periodic time of any orb DIO is reciprocally as the area DdQ,, that is (by the known methods of quadratures), directly as the square of the distance SD.

Which was first to be demonstrated.

CASE 2

Drawn many indefinite right lines from the sphere’s center. These revolve around the axis.

The orbs are to be cut into innumerable annuli.

Every annulus has 4 annuli contiguous to it.

• One on its inside
• One on its outside
• 2 on each hand.

Each of these annuli cannot be impelled equally and with contrary directions by the attrition of the interior and exterior annuli.

• This is unless the motion be communicated according to the law demonstrated in Case 1.
• This appears from that demonstration.

Therefore any series of annuli, taken in any right line extending itself in inflnitum from the globe, will move according to the law of Case 1, except we should imagine it hindered by the attrition of the annuli on each side of it.

But now in a motion, according to this law, no such is, and therefore cannot be, any obstacle to the motions persevering according to that law.

If annuli at equal distances from the centre revolve either more swiftly or more slowly near the poles than near the ecliptic, they will be accelerated if slow, and retarded if swift, by their mutual attrition;

And so the periodic times will continually approach to equality, according to the law of Case 1.

Therefore, this attrition will not at all hinder the motion from going on according to the law of Case 1.

• Therefore that law will take place.

The periodic times of the several annuli will be as the squares of their distances from the centre of the globe. Which was to be demonstrated in the second place.

CASE 3

Divide every annulus by transverse sections into innumerable particles constituting a substance absolutely and uniformly fluid.

These sections do not at all respect the law of circular motion. They only produce a fluid substance. And so the law of circular motion will continue the same as before.

All the very small annuli will either not at all change their asperity and force of mutual attrition because of these sections.

• Otherwise, they will change the same equally.

Therefore, the proportion of the causes remain the same.

• Thus, the proportion of the motions and the periodic times, as effects, will remain the same also. Q.E.D.

But now, the circular motion and the centrifugal force arising would be greater at the ecliptic than at the poles.

So there must be some cause operating to retain the several particles in their circles.

Otherwise, the matter that is at the ecliptic will:

• always move away from the centre
• come round to the poles by the outside of the vortex
• return from there by the axis to the ecliptic with a perpetual circulation.