Proposition 44, Theorem 35

Assume that:

• water ascends and descends alternately in the erected legs KL, MN, of a pipe.
• a pendulum has a length between the point of suspension and the centre of oscillation equal to half the length of the water in the canal

The water will ascend and descend in the same times in which the pendulum oscillates.

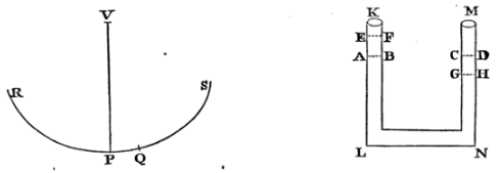
I measure the length of the water along the axes of the canal and its legs, and make it equal to the sum of those axes; and take no notice of the resistance of the water arising from its attrition by the sides of the canal.

Let, therefore, AB, CD, represent the mean height of the water in both legs; and when the water in the leg KL ascends to the height EF, the water will descend in the leg MN to the height GH. Let P be a pendulous body, VP the thread, V the point of suspension, RPQS the cycloid which the pendulum describes, P its lowest point, PQ an arc equal to the height AE. The force with which the motion of the water is accelerated and retarded alternately is the excess of the weight of the water in one leg above the weight in the other;

Therefore, when the water in the leg KL ascends to EF, and in the other leg descends to GH, that force is double the weight of the water EABF, and therefore is to the weight of the whole water as AE or PQ to VP or PR.

The force also with which the body P is accelerated or retarded in any place, as Q, of a cycloid, is (by Cor. Prop. LI) to its whole weight as its distance PQ from the lowest place P to the length PR of the cycloid.

Therefore the motive forces of the water and pendulum, draws the equal spaces AE, PQ, are as the weights to be moved; and therefore if the water and pendulum are quiescent at first, those forces will move them in equal times, and will cause them to go and return together with a reciprocal motion. Q.E.D.

Corillary 1

Therefore the reciprocations of the water in ascending and descending are all performed in equal times, whether the motion be more or less intense or remiss.

Corillary 2

If the length of the whole water in the canal be of 6 1/9 French feet, the water will descend in 1 second, and will ascend in another second, and so on by turns infinitely. For a pendulum of 3 1/18 such feet in length will oscillate in one second of time.

Corillary 3

But if the length of the water be increased or diminished, the time of the reciprocation will be increased or diminished in the subduplicate ratio of the length.

PROPOSITION XLV. THEOREM XXXVI.

The velocity of waves is in the subduplicate ratio of the breadths.

This follows from the construction of the following Proposition.