Proposition 41, Theorem 32

PROPOSITION 41. THEOREM 32

A pressure is not propagated through a fluid in rectilinear directions unless where the particles of the fluid lie in a right line.

Assume that the particles a, b, c, d, e lie in a right line.

The pressure can be directly propagated from a to e.

But then the particle e will urge the obliquely posited particles f and g obliquely.

Particles f and g will not sustain this pressure unless they be supported by the particles h and k lying beyond them.

But the particles that support them are also pressed by them.

Those particles cannot sustain that pressure, without being supported by, and pressing on, those particles that lie still farther, as l and m, and so on infinitely.

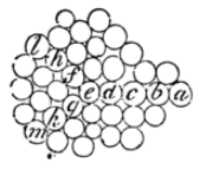
Therefore the pressure propagated to particles that lie out of right lines begins to deflect towards one hand and the other.

It will be propagated obliquely infinitely.

After it has begun to be propagated obliquely, if it reaches more distant particles lying out of the right line, it will deflect again on each hand.

This it will do as often as it lights on particles that do not lie exactly in a right line. Q.E.D.

Corollary

If any part of a pressure, propagated through a fluid from a given point, be intercepted by any obstacle, the remaining part, which is not intercepted, will deflect into the spaces behind the obstacle. This may be demonstrated also after the following manner.

Let a pressure be propagated from the point A towards any part, and, if it be possible, in rectilinear directions; and the obstacle NBCK being perforated in BC, let all the pressure be intercepted but the coniform part APQ passing through the circular hole BC. Let the cone APQ be divided into frustums by the transverse plants, de, fg, hi.

Then while the cone ABC, propagating the pressure, urges the conic frustum degf beyond it on the superficies de, and this frustum urges the next frustum fgih on the superficies fg, and that frustum urges a third frustum, and so in infinitum; it is manifest (by the third Law) that the first frustum defg is, by the re-action of the second frustum fghi, as much urged and pressed on the superficies fg, as it urges and presses that second frustum. Therefore the frustum degf is compressed on both sides, that is, between the cone Ade and the frustum fhig; and therefore (by Case 6, Prop. XIX) cannot preserve its figure, unless it be compressed with the same force on all sides. Therefore with the same force with which it is pressed on the superficies de, fg, it will endeavour to break forth at the sides df, eg; and there (being not in the least tenacious or hard, but perfectly fluid) it will run out, expanding itself, unless there be an ambient fluid opposing that endeavour. Therefore, by the effort it makes to run out, it will press the ambient fluid, at its sides df, eg, with the same force that it does the frustum fghi; and therefore, the pressure will be propagated as much from the sides df, eg, into the spaces NO, KL this way and that way, as it is propagated from the superficies fg towards PQ. Q.E.D.