Proposition 3 Problem 1

Proposition 3 Problem 1

Define the motion of a body which, in a similar medium:

• rises or falls in a right line
• is resisted in the ratio of its speed
• acted on by a uniform force of gravity.

When the body rises, the gravity is expounded by any given rectangle BACH.

The resistance of the medium, at the beginning of the ascent, by the rectangle BADE. This is taken on the contrary side of the right line AB.

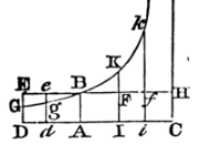
Through the point B, with the rectangular asymptotes AC, CH, draw a hyperbola that cuts the perpendiculars DE, de, in G, g.

The rising body will:

• in the time DGgd describe the space EGge.
• in the time DGBA draw the space of the whole ascent EGB
• in the time ABKI draw the space of descent BFK
• in the time IKki the space of descent KFfk

The speeds of the bodies (proportional to the resistance of the medium) in these periods of time will be ABED, ABed, O, ABFI, ABfi respectively.

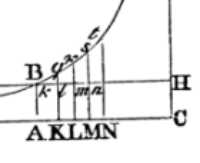
The greatest velocity which the body can acquire by descending will be BACH.

The rectangle BACH is resolved into innumerable rectangles Ak, Kl, Lm, Mn, etc.

These shall be as the increments of the speeds produced in so many equal times.

Then will 0, Ak, Al, Am, An, &c., be as the whole velocities; and therefore (by supposition) as the resistances of the medium in the beginning of each of the equal times.

Make AC to AK, or ABHC to ABkK, as the force of gravity to the resistance in the beginning of the second time; then from the force of gravity subduct the resistances, and ABHC, KkHC, LlHC, MmHC, &c., will be as the absolute forces with which the body is acted upon in the beginning of each of the times, and therefore (by Law I) as the increments of the velocities, that is, as the rectangles Ak, Kl, Lm, Mn, &c., and therefore (by Lem. 1, Book II) in a geometrical progression.

Therefore, if the right lines Kk, Ll, Mm, Nn, &c., are produced so as to meet the hyperbola in q, r, s, t, &c. the areas ABqK, KqrL, LrsM, MstN, &c., will be equal, and therefore analogous to the equal times and equal gravitating forces.

But the area ABqK (by Corol. 3, Lem. VII and VIII, Book I) is to the area Bkq as Kq to ½kq, or AC to ½AK, that is, as the force of gravity to the resistance in the middle of the first time. And by the like reasoning, the areas qKLr, rLMs, sMNt, &c., are to the areas qklr, rlms, smnt, &c., as the gravitating forces to the resistances in the middle of the second, third, fourth time, and so on.

Therefore since the equal areas BAKq, qKLr, rLMs, sMNt, &c., are analogous to the gravitating forces, the areas Bkq, qklr, rlms, smnt, &c., will be analogous to the resistances in the middle of each of the times, that is (by supposition), to the velocities, and so to the spaces described.

Take the sums of the analogous quantities, and the areas Bkq, Blr, Bms, But, &c., will be analogous to the whole spaces described; and also the areas ABqK, ABrL, ABsM, ABtN, &c., to the times. Therefore the body, in descending, will in any time ABrL describe the space Blr, and in the time LrtN the space rlnt. Q.E.D.

The like demonstration holds in ascending motion.

Corollary 1

Therefore, the greatest velocity that the body can acquire by falling is to the velocity acquired in any given time as the given force of gravity which perpetually acts upon it to the resisting force which opposes it at the end of that time.

Corollary 2

But the time being augmented in an arithmetical progression, the sum of that greatest velocity and the velocity in the ascent, and also their difference in the descent, decreases in a geometrical progression.

Corollary 3

Also the differences of the spaces, which are described in equal differences of the times, decrease in the same geometrical progression.

Corollary 4

The space described by the body is the difference of two spaces, whereof one is as the time taken from the beginning of the descent, and the other as the velocity; which [spaces] also at the beginning of the descent are equal among themselves.