Proposition 1-2 Theorem 1-2

Proposition 1 Theory 1

If a body is resisted in the ratio of its velocity, the motion lost by resistance is as the space gone over in its motion.

For since the motion lost in each equal particle of time is as the velocity, that is, as the particle of space gone over, then, by composition, the motion lost in the whole time will he as the whole space gone over.

Corollary

Therefore if the body, destitute of all gravity, move by its innate and there be given both its whole motion at the beginning, and also the motion remaining after some part of the way is gone over, there will be given also the whole space which the body can describe in an infinite time.

For that space will be to the space now described as the whole force only in free spaces, motion at the beginning is to the part lost of that motion.

Lemma 1

Quantities proportional to their differences are continually proportional.

Let A be to A - B as B to B - C and C to C - D, &c., and, by conversion, A will be to B as B to C and C to D, &c. Q.E.D.

PROPOSITION 2 Theorem 2

If a body is resisted in the ratio of its velocity, and moves, by its vis insita only, through a similar medium, and the times be taken equal, the velocities in the beginning of each of the times are in a geometrical progression, and the spaces described in each of the times are as the velocities.

Case 1

Let the time be divided into equal particles.

If at the very beginning of each particle we suppose the resistance to act with one single impulse which is as the velocity, the decrement of the velocity in each of the particles of time will be as the same velocity.

Therefore, the velocities are proportional to their differences, and therefore (by Lem. 1, Book II) continually proportional.

Therefore, if out of an equal number of particles there be compounded any equal portions of time, the velocities at the beginning of those times will be as terms in a continued progression, which are taken by intervals, omitting every where an equal number of intermediate terms.

But the ratios of these terms are compounded of the equal ratios of the intermediate terms equally repeated, and therefore are equal.

Therefore the velocities, being proportional to those terms, are in geometrical progression.

Let those equal particles of time be diminished, and their number increased in infinitum, so that the impulse of resistance may become continual.

The velocities at the beginnings of equal times, always continually proportional, will be also in this case continually proportional. Q.E.D.

Case 2

By division, the differences of the velocities, that is, the parts of the velocities lost in each of the times, are as the wholes; but the spaces described in each of the times are as the lost parts of the velocities (by Prop. 1, Book I), and therefore are also as the wholes. Q.E.D.

Corollary

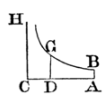
Hence if to the rectangular asymptotes AC, CH, the hyperbola BG is described, and AB, DG is drawn perpendicular to the asymptote AC, and both the velocity of the body, and the resistance of the medium, at the very beginning of the motion, be expressed by any given line AC, and, after some time is elapsed, by the indefinite line DC;

The time may be expressed by the area ABGD, and the space described in that time by the line AD. For if that area, by the motion of the point D, be uniformly increased in the same manner as the time, the right line DC will decrease in a geometrical ratio in the same manner as the velocity; and the parts of the right line AC, described in equal times, will decrease in the same ratio.