Proposition 37 Theorem 26

To define the times of the ascent or descent of a body projected upwards or downwards from a given place.

Suppose the body to go off from the given place G, in the direction of the line GS, with any velocity. In the duplicate ratio of this velocity to the uniform velocity in a circle, with which the body may revolve about the centre S at the given interval SG, take GA to ½AS.

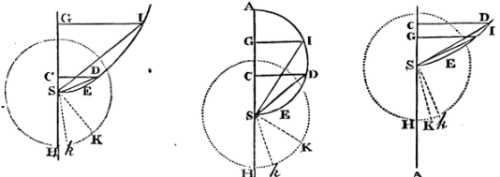
If that ratio is the same as of the number 2 to 1, the point A is infinitely remote; in which case a parabola is to be described with any latus rectum to the vertex S, and axis SG; as appears by Prop. XXXIV. But if that ratio is less or greater than the ratio of 2 to 1, in the former case a circle, in the latter a rectangular hyperbola, is to be described on the diameter SA; as appears by Prop. XXXIII. Then about the centre S, with an interval equal to half the latus rectum, describe the circle HkK; and at the place G of the ascending or descending body, and at any other place C, erect the perpendiculars GI, CD, meeting the conic section or circle in I and D. Then joining SI, SD, let the sectors HSK, HSk be made equal to the segments SEIS, SEDS, and (by Prop. XXXV) the body G will describe the space GC in the same time in which the body K may describe the arc Kk. Q.E.F.

PROPOSITION 38 Theorem 12

Supposing that the centripetal force is proportional to the altitude or distance of places from the centre. I say, that the times and velocities of falling bodies, and the spaces which they describe, are respectively proportional to the arcs, and the right and versed sines of the arcs.

Suppose the body to fall from any place A in the right line AS; and about the centre of force S, with the interval AS, describe the quadrant of a circle AE; and let CD be the right sine of any arc AD; and the body A will in the time AD in falling describe the space AC, and in the place C will acquire the velocity CD.

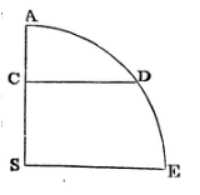
This is demonstrated the same way from Prop. X, as Prop. XXXII was demonstrated from Prop. XI.

Cor. 1

Hence the times are equal in which one body falling from the place A arrives at the centre S, and another body revolving describes the quadrantal arc ADE.

Cor. 2

All the times are equal in which bodies falling from whatsoever places arrive at the centre.

For all the periodic times of revolving bodies are equal (by Cor. 3, Prop. IV).