Proposition 35 Theorem 40

The area of the figure DES, described by the indefinite radius SD, is equal to the area which a body with a radius equal to half the latus rectum of the figure DES, by uniformly revolving about the centre S, may describe in the same time.

A body C in the smallest moment of time describes in falling the infinitely little line Cc. while another body K, uniformly revolving around the center S in the circle OKk, describes the arc Kk.

Erect the perpendiculars CD, cd, meeting the figure DES in D, d.

Join SD, Sd, SK, Sk, and draw Dd meeting the axis AS in T, and thereon let fall the perpendicular SY.

Case 1

If DES is a circle, or a rectangular hyperbola, bisect its transverse diameter AS in O, and SO will be half the latus rectum. And because TC is to TD as Cc to Dd, and TD to TS as CD to SY; ex æquo TC will be to TS as CD x Cc to SY x Dd.

But (by Cor. 1, Prop. XXXIII) TC is to TS as AC to AO; to wit, if in the coalescence of the points D, d, the ultimate ratios of the lines are taken. Wherefore AC is to AO or SK as CD x Cc to SY x Dd.

Farther, the velocity of the descending body in C is to the velocity of a body describing a circle about the centre S, at the interval SC, in the subduplicate ratio of AC to AO or SK (by Prop. XXXIII); and this velocity is to the velocity of a body describing the circle OKk in the subduplicate ratio of SK to SC (by Cor. 6, Prop IV); and, ex æquo, the first velocity to the last, that is, the little line Cc to the arc Kk, in the subduplicate ratio of AC to SC, that is, in the ratio of AC to CD. Wherefore CD x Cc is equal to AC × Kk.

Consequently AC to SK as AC × Kk to SY × Dd.

Thence SK × Kk equal to SY × Dd, and ½SK × Kk equal to ½SY × Dd, that is, the area KSk equal to the area SDd.

Therefore in every moment of time two equal particles, KSk and SDd, of areas are generated, which, if their magnitude is diminished, and their number increased in infinitum, obtain the ratio of equality, and consequently (by Cor. Lem. IV), the whole areas together generated are always equal. Q.E.D.

Case 2

But if the figure DES is a parabola, we shall find, as above, CD × Cc to SY × Dd as TC to TS, that is, as 2 to 1; and that therefore ¼CD × Cc is equal to ½SY × Dd.

But the velocity of the falling body in C is equal to the velocity with which a circle may be uniformly described at the interval ½SC (by Prop. XXXIV).

This velocity to the velocity with which a circle may be described with the radius SK, that is, the little line Cc to the arc Kk, is (by Cor. 6, Prop. IV) in the subduplicate ratio of SK to ½SC; that is, in the ratio of SK to ½CD. Wherefore ½SK × Kk is equal to ¼CD × Cc, and therefore equal to ½SY × Dd; that is, the area KSk is equal to the area SDd, as above. Q.E.D.

PROPOSITION 36 PROBLEM 25

Determine the time of the fall of a body from a place A

Upon the diameter AS, the distance of the body from the centre at the beginning, likewise the semi-circle describe the semi-circle OKH equal thereto, about the centre S.

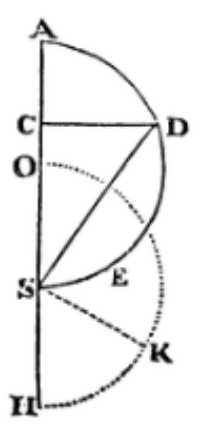
From any place C of the body erect the ordinate CD.

Join SD, and make the sector OSK equal to the area ASD. It is evident (by Prop. XXXV) that the body in falling will describe the space AC in the same time in which another body, uniformly revolving about the centre S, may describe the arc OK. Q.E.F.