Elliptic trajectory
Table of Contents
Proposition 31 Problem 23: Find the place of a body moving in an elliptic trajectory
Let:
- A the principal vertex
- S the focus
- O the centre of the ellipsis APB
- P is the place where the body is found
Produce OA to G so as OG may be to OA as OA to OS. Erect the perpendicular GH.
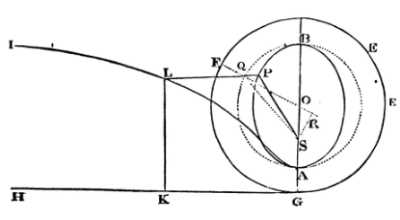
Around bout the centre O, with the interval OG, describe the circle GEF; and on the ruler GH, as a base, suppose the wheel GEF to move forwards, revolving about its axis, and in the mean time by its point A describing the cycloid ALI. Which done, take GK to the perimeter GEFG of the wheel, in the ratio of the time in which the body proceeding from A described the arc AP, to the time of a whole revolution in the ellipsis. Erect the perpendicular KL meeting the cycloid in L; then LP drawn parallel to KG will meet the ellipsis in P, the required place of the body.
For about the centre O with the interval OA describe the semi-circle AQB, and let LP, produced, if need be, meet the arc AQ in Q, and join SQ, OQ. Let OQ meet the arc EFG in F, and upon OQ let fall the perpendicular SR. The area APS is as the area AQS, that is, as the difference between the sector OQA and the triangle OQS, or as the difference of the rectangles ½OQ
…
that is, because ½OQ is given, as the difference between the arc AQ and the right line SR; and therefore (because of the equality of the given ratios SR to the sine of the arc AQ, OS to OA, OA to OG, AQ to GF; and by division, AQ - SR to GF - sine of the arc AQ) as GK, the difference between the arc GF and the sine of the arc AQ. Q.E.D.
Scholium
A description of this curve is difficult. A solution by approximation will be preferable.
First, let there be found a certain angle B which may be to an angle of 57,29578 degrees, which an arc equal to the radius subtends, as SH, the distance of the foci, to AB, the diameter of the ellipsis. Secondly, a certain length L, which may be to the radius in the same ratio inversely.
These being found, the Problem may be solved by the following analysis.
By any construction (or even by conjecture), suppose we know P the place of the body near its true place p. Then letting fall on the axis of the ellipsis the ordinate PR from the proportion of the diameters of the ellipsis, the ordinate RQ of the circumscribed circle AQB will be given; which ordinate is the sine of the angle AOQ, supposing AO to be the radius, and also cuts the ellipsis in P.
It will be sufficient if that angle is found by a rude calculus in numbers near the truth. Suppose we also know the angle proportional to the time, that is, which is to four right angles as the time in which the body described the arc Ap, to the time of one revolution in the ellipsis.
Let this angle be N. Then take an angle D, which may be to the angle B as the sine of the angle AOQ to the radius; and an angle E which may be to the angle N - AOQ + D as the length L to the same length L diminished by the cosine of the angle AOQ, when that angle is less than a right angle, or increased thereby when greater.
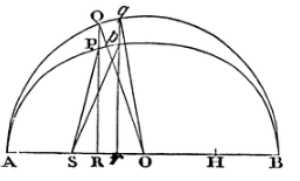
In the next place, take an angle F that may be to the angle B as the sine of the angle AOQ + E to the radius, and an angle G, that may be to the angle N - AOQ - E + F as the length L to the same length L diminished by the cosine of the angle AOQ + E, when that angle is less than a right angle, or increased thereby when greater. For the third time take an angle H, that may be to the angle B as the sine of the angle AOQ + E + G to the radius; and an angle I to the angle N - AOQ - E - G + H, as the length L is to the same length L diminished by the cosine of the angle AOQ + E + G, when that angle is less than a right angle, or increased thereby when greater.
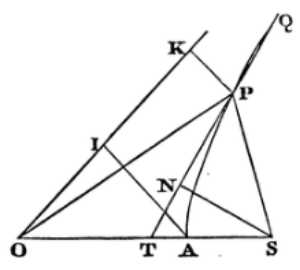
And so we may proceed in infinitum. Lastly, take the angle AOq equal to the angle AOQ + E + G + I +, &c. and from its cosine Or and the ordinate pr, which is to its sine qr as the lesser axis of the ellipsis to the greater, we shall have p the correct place of the body. When the angle N - AOQ + D happens to be negative, the sign + of the angle E must be every where changed into -, and the sign - into +. And the same thing is to be understood of the signs of the angles G and I, when the angles N - AOQ - E + F, and N - AOQ - E - G + H come out negative. But the infinite series AOQ + E + G + I +, &c. converges so very fast, that it will be scarcely ever needful to proceed beyond the second term E. And the calculus is founded upon this Theorem, that the area APS is as the difference between the arc AQ and the right line let fall from the focus S perpendicularly upon the radius OQ.
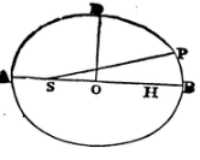
Let its centre be O, its vertex A, its focus S, and asymptote OK; and suppose the quantity of the area to be cut off is known, as being proportional to the time. Let that be A, and by conjecture suppose we know the position of a right line SP, that cuts off an area APS near the truth. Join OP, and from A and P to the asymptote draw AI, PK parallel to the other asymptote; and by the table of logarithms the area AIKP will be given, and equal thereto the area OPA, which subducted from the triangle OPS, will leave the area cut off APS. And by applying 2APS - SA, or 2A - SAPS, the double difference of the area A that was to be cut off, and the area APS that is cut off, to the line SN that is let fall from the focus S, perpendicular upon the tangent TP, we shall have the length of the chord PQ. Which chord PQ is to be inscribed between A and P, if the area APS that is cut off be greater than the area A that was to be cut off, but towards the contrary side of the point P, if otherwise: and the point Q will be the place of the body more accurately. And by repeating the computation the place may be found perpetually to greater and greater accuracy.
And by such computations we have a general analytical resolution of the Problem. But the particular calculus that follows is better fitted for astronomical purposes. Supposing AO, OB, OD, to be the semi-axis of the ellipsis, and L its latus rectum, and D the difference betwixt the lesser semi-axis OD, and ½L the half of the latus rectum: let an angle Y be found, whose sine may be to the radius as the rectangle under that difference D, and AO + OD the half sum of the axes to the square of the greater axis AB. Find also an angle Z, whose sine may be to the radius as the double rectangle under the distance of the foci SH and that difference D to triple the square of half the greater semi-axis AO.
Those angles being once found, the place of the body may be thus determined. Take the angle T proportional to the time in which the arc BP was described, or equal to what is called the mean motion; and an angle V the first equation of the mean motion to the angle Y, the greatest first equation, as the sine of double the angle T is to the radius; and an angle X, the second equation, to the angle Z, the second greatest equation, as the cube of the sine of the angle T is to the cube of the radius. Then take the angle BHP the mean motion equated equal to T + X + V, the sum of the angles T, V, X, if the angle T is less than a right angle; or equal to T + X - V, the difference of the same, if that angle T is greater than one and less than two right angles; and if HP meets the ellipsis in P, draw SP, and it will cut off the area BSP nearly proportional to the time.
This practice seems to be expeditious enough, because the angles V and X, taken in second minutes, if you please, being very small, it will be sufficient to find two or three of their first figures. But it is likewise sufficiently accurate to answer to the theory of the planet’s motions.
In the orbit of Mars, the greatest equation of the centre amounts to 10 degrees.
- The error will scarcely exceed 1 second.
But when the angle of the mean motion equated BHP is found, the angle of the true motion BSP, and the distance SP, are readily had by the known methods.