Proposition 30 Problem 22

Proposition 30 Problem 22

Find at any time the place of a body moving in a given parabolic trajectory.

Let:

• S be the focus
• A the principal vertex of the parabola

Suppose 4AS x M equal to the parabolic area to be cut off APS, which either was described by the radius SP, since the body’s departure from the vertex, or is to be described thereby before its arrival there.

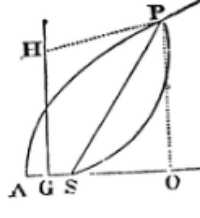
The quantity of that area to be cut off is known from the time which is proportional to it.

Bisect AS in G, and erect the perpendicular GH equal to 3M, and a circle described about the centre H, with the interval HS, will cut the parabola in the place P required. For letting fall PO perpendicular on the axis, and drawing PH, there will be AG² + GH² (= HP² =

= AO² + PO² - 2GAO + 2 GH + PO + AG² + GH². Whence 2GH

PO (=AO² + PO² - 2GAO) = AO² + ¾PO². For AO² write

then dividing all the terms by 3PO, and multiplying them by 2AS, we shall have 4/3GH

PO = to the area

= to the area APS. But GH was 3M, and therefore 4/3GH

AS is 4AS

M. Wherefore the area cut off APS is equal to the area that was to be cut off 4AS

Q.E.D.

Cor. 1

Hence GH is to AS as the time in which the body drawn the arc AP to the time in which the body described the arc between the vertex A and the perpendicular erected from the focus S on the axis.

Cor. 2

A circle ASP perpetually passes through the moving body P.

The speed of point H is to the speed which the body had in vertex A as 3 to 8.

Therefore in the same ratio is the line GH to the right line which the body, in the time of its moving from A to P, would draw with that speed which it had in vertex A.

Cor. 3

Hence, the time may be found in which the body has drawn any assigned arc AP.

Join AP, and on its middle point erect a perpendicular meeting the right line GH in H.