Scholium

Galileo discovered Law 1, 2, and Corollaries 1, 2 as bodies:

• falling in the duplicate ratio of the time [as seconds squared]
• moving in a parabola as projectiles

The uniform gravity of a body acts equally in equal particles of time on that body to create equal velocities. In the whole time, gravity impresses a whole force and generates a velocity proportional to that time.

The space traveled per time are proportional to the velocity and time together in a duplicate ratio of the times*.

When a body is thrown upwards, its uniform gravity:

• impresses forces
• removes its upward soeeds.

At the highest point, all the upward speeds [in unity] are removed.

If a body is projected in any direction, the resulting motion is compounded with the motion arising from its gravity.

The body A by its motion of projection alone draws in a given time the right line AB.

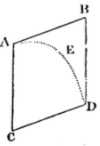
Its motion of falling alone draws the altitude AC in the same time.

The body in paralellogram ABDC by that compounded motion will at the end of the time be at place D.

It will draw AED, a parabola, to which the right line AB will be a tangent in A.

Its ordinate BD will be as the square of the line AB.

Those same Laws and Corollaries are demonstrated by the times of the vibration of pendulums and pendulum clocks.

The greatest geometers of our times are:

• Sir Christ. Wren
• Dr. Wallis
• Mr. Huygens

They, with the third Law, determined the rules of the congress and reflexion of hard bodies.

• These agree with my rules.

Dr. Wallis achieved this first, then Sir Christopher Wren, and lastly, Mr. Huygens.

To bring this experiment in accurate agreement with my theory, we should regard air resistance as to the elastic force of the concurring bodies.

Let the spherical bodies A, B be suspended by the parallel and equal strings AC, BD, from the centres C, D.

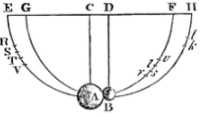
Around these centres, with those intervals, describe the semicircles EAF, GBH, bisected by the radii CA, DB.

Bring the body A to any point R of the arc EAF.

Withdraw the body B and let A go from there.

After 1 oscillation it returns to the point V.

RV will be the retardation arising from the air resistance.

Of this RV let ST be a fourth part, situated in the middle. In this way, RS and TV are equal and RS is to ST as 3 to 2.

Then ST will represent very nearly the retardation during the descent from S to A.

Return body B to its place.

Let body A fall from point S.

Its speed in the place of reflexion A will be the same as if it had fallen in vacuo from the point T.

This speed may be represented by the chord of the arc TA.

Geometers know that the speed of a pendulous body in the lowest point is as the chord of the arc which it has drew in its fall.

After reflexion, suppose:

• body A comes to the place s
• body B comes to the place k.

Withdraw the body B and find the place v. From there if body A is let go, it should after 1 oscillation return to the place r, st may be a fourth part of rv, so placed in the middle thereof as to leave rs equal to tv.

Let the chord of the arc tA represent the velocity which body A had in the place A immediately after reflexion.

For t will be the true and correct place to which the body A should have ascended, if the resistance of the air had been taken off.

In the same way we are to correct the place k to which the body B ascends, by finding the place l to which it should have ascended in vacuo.

Thus everything may be subjected to experiment, in the same manner as if we were really placed in vacuo.

Take the product of the body A by the chord of the arc TA which represents its speed. So we have its motion in the place A immediately before reflexion.

And then by the chord of the arc tA, that we may have its motion in the place A immediately after reflexion.

We are to take the product of body B by the chord of the arc Bl, that we may have the motion of the same immediately after reflexion.

Similarly, when 2 bodies are let go together from different places, we are to find the motion of each, as well before as after reflexion.

Then we may compare the motions between themselves, and collect the effects of the reflexion.