Corollaries 1-2

Corollary 1

• A force M impressed on a body at A will be uniformly carried from A to B.
• A force N impressed at A will be carried from A to C.
• If N and M act together, their forces will an the same time be carried in the diagonal from A to D.
  • Law 2 means that N will not at all change the velocity generated by M
  • The body therefore will arrive at the line BD in the same time, whether the force N be impressed or not. Therefore at the end of that time, it will be found somewhere in the line BD.
• Likewise, it will be found somewhere in the line CD at the end of the same time, if N were impressed. Therefore, it will be in the point D where both lines meet.
  • But Law 1 means that it will move from A to D.

Corollary 2

As if the unequal radii OM and ON drawn from the centre O of any wheel, should sustain the weights A and P by the cords MA and NP; and the forces of those weights to move the wheel were required. Through the centre O draw the right line KOL, meeting the cords perpendicularly in K and L;

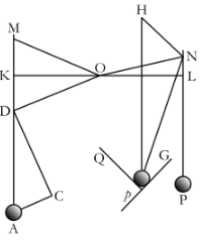
From the centre O, with OL the greater of the distances OK and OL, describe a circle, meeting the cord MA in D: and drawing OD, make AC parallel and DC perpendicular thereto. Now, it being indifferent whether the points K, L, D, of the cords be fixed to the plane of the wheel or not, the weights will have the same effect whether they are suspended from the points K and L, or from D and L. Let the whole force of the weight A be represented by the line AD, and let it be resolved into the forces AC and CD; of which the force AC, drawing the radius OD directly from the centre, will have no effect to move the wheel: but the other force DC, drawing the radius DO perpendicularly, will have the same effect as if it drew perpendicularly the radius OL equal to OD; that is, it will have the same effect as the weight P, if that weight is to the weight A as the force DC is to the force DA; that is (because of the similar triangles ADC, DOK), as OK to OD or OL. Therefore the weights A and P, which are reciprocally as the radii OK and OL that lie in the same right line, will be equipollent, and so remain in equilibrio; which is the well known property of the balance, the lever, and the wheel. If either weight is greater than in this ratio, its force to move the wheel will be so much greater.

If the weight p, equal to the weight P, is partly suspended by the cord Np, partly sustained by the oblique plane pG; draw pH, NH, the former perpendicular to the horizon, the latter to the plane pG; and if the force of the weight p tending downwards is represented by the line pH, it may be resolved into the forces pN, HN. If there was any plane pQ, perpendicular to the cord pN, cutting the other plane pG in a line parallel to the horizon, and the weight p was supported only by those planes pQ, pG, it would press those planes perpendicularly with the forces pN; HN; to wit, the plane pQ with the force pN, and the plane pG with the force HN. And therefore if the plane pQ was taken away, so that the weight might stretch the cord, because the cord, now sustaining the weight, supplies the place of the plane that was removed, it will be strained by the same force pN which pressed upon the plane before. Therefore, the tension of this oblique cord pN will be to that of the other perpendicular cord PN as pN to pH. And therefore if the weight p is to the weight A in a ratio compounded of the reciprocal ratio of the least distances of the cords PN, AM, from the centre of the wheel, and of the direct ratio of pH to pN, the weights will have the same effect towards moving the wheel, and will therefore sustain each other; as any one may find by experiment.

But the weight p pressing upon those two oblique planes, may be considered as a wedge between the two internal surfaces of a body split by it; and hence the forces of the wedge and the mallet may be determined; for because the force with which the weight p presses the plane pQ is to the force with which the same, whether by its own gravity, or by the blow of a mallet, is impelled in the direction of the line pH towards both the planes, as pN to pH; and to the force with which it presses the other plane pG, as pN to NH. And thus the force of the screw may be deduced from a like resolution of forces; it being no other than a wedge impelled with the force of a lever. Therefore the use of this Corollary spreads far and wide, and by that diffusive extent the truth thereof is farther confirmed. For on what has been said depends the whole doctrine of mechanics variously demonstrated by different authors. For from hence are easily deduced the forces of machines, which are compounded of wheels, pullies, levers, cords, and weights, ascending directly or obliquely, and other mechanical powers; as also the force of the tendons to move the bones of animals.