The Construction Of Regular Shapes

Part 1: Planes

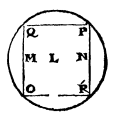
A plane figure is regular if it has all its sides and all its outward-facing angles equal to one another as below:

Part 2: Stars

Some of these shapes are primary and basic, not extending beyond their boundaries.

Others are augmented, extending beyond their sides

If 2 non-neighboring sides of one of the basic figures are produced, they meet to form a vertex of the augmented figure. These are called Stars.

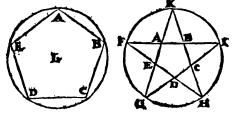
ABODE is a perfect 5-cornered shape figure, a primary figure. It does not require any completion which might result from producing its sides.

FGHIK is a 5-cornered star, an augmented figure. It is constricted by producing pairs of non-neighboring sides, such as AB and DC produced to meet at I.

Part 3: Semiregular Shapes

Shapes are semiregular if their angles are different from one another but they have 4 equal sides, like the Rhombi NMPO, GEKD.

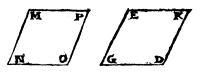
Proposition 4

All regular shapes can be placed so that all their angles simultaneously lie on the same circle

Euclid (III.21) states that all equal angles can be inscribed in the same segment, and thus also in equal segments of the same circle, and all the angles of a Regular shape are equal, so all the angles of one figure can be inscribed in equal segments of one circle.

But in fact it is necessary that, if one is inscribed, it should be possible to inscribe them all.

All the sides are equal. Therefore, the segments of the circle cut off by the 2 sides around 1 angle are equal, by Euclid III.24.

Therefore, as the angle fits, so do the extremities of the sides fit in the same circle. The extremities of the sides are the angles.

It would be otherwise, if, although the angles were equal the sides were not equal, for then the necessity that it should be possible to inscribe them all would disappear.

Part 5: Drawing a Shape

Drawing a Shape is to construct the Elementary triangles of the figure and fit the triangles together to complete the figure.

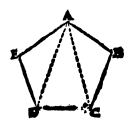
Given the ratio of DA to AE, ED, we form the triangles DAE, DAC, CAB:from which thefigure is built up.

Part 6: Definition

To draw a shape in a circle we must by Geometrical means determine the ratio of the side of the figure to the diameter of the circle in which it is to be inscribed, and when we have established this ratio the proposed figure is easily drawn in the circle.

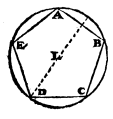
As, if we are given the semidiameter LD, or diameter twice LD, if we know how to obtain from it the correct length for the side DE we can then, by repeatedly taking this length DE round the circumference, easily draw the whole figure.

Part 7: Definition

In geometrical matters, to know is to measure by a known measure, which known measure in our present concern, the inscription of shaes in a circle, is the diameter of the circle.