Mars' Orbit is Ellipse

The libration has been established and proven as in Chapter 56. Nevertheless, an error can be admitted in the improper application of the libration, by which the path of the planet is made uneven.

What I have aimed at throughout this entire work is to find a physical hypothesis that would not only produce distances consonant with observations, but also equations that are likewise sound, which up to now we have been compelled to borrow vicariously from Chapter 16.

The path of the planets is an ellipse, not an oval path.

In the line of apsides, with centers A and B, let equal circles GD and HK be drawn.

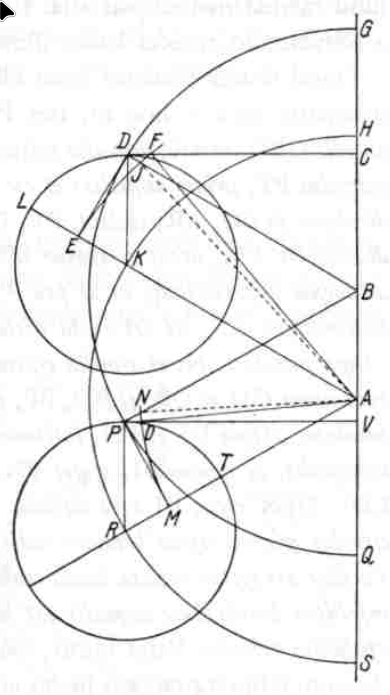
Let AB be the eccentricity of circle GD.

But let the anomaly of the eccentric, or the number of its degrees, be the arc GD or HK, for equivalence of chapter 3.

Therefore, center K, with interval KD, which is equal to AB itself, let the epicycle LDF be drawn. This will cut circle GD at D, for equivalence of chapter 3.

Let AK be drawn, and let it be continued until it cuts the epicycle at L, so that LD is an arc similar to the anomaly of the eccentricity GD or HK.

Let B be connected with D.

From point D, however, let perpendiculars be dropped to GA, LA, which are DC, DE.

Therefore, by what has been demonstrated up to this point in chapter 56, AE will undoubtedly be the just distance to this anomaly of the eccentricity, about which it is sought, how much time is consumed in it, since the sine of its arc versus GC, or after multiplication, LE subtracted from GA, revealed the just distance AE.

From these indications I was persuaded that the other end of AE itself, which must be sought, is not on line DC, which was nevertheless very true, but at point I of line DB: as if with center A, with interval AE, I were to draw arc EIF, which cuts DB at I.

Therefore, according to this persuasion, AI would be the just distance, in position and length, and IAG truly equated anomaly.

But it is manifest that arc EIF intersects line DC, in the place above, namely at F. So the angles IAG and FAG differ by the quantity IAF.

Therefore, I erred, having used line AI for AF. The error was first detected by experience.

For when I had explored the quantity of area DAG both by all the distances and by small area DAB, then afterwards I accommodated angle IAG, not FAG, to this area DAG converted into time; then in the upper part of the semicircle I collected by 5½ more, in the lower part by 4 minutes less, than the vicarage gave, quite certain.

So, since the equations disagreed with the truth, I began again to accuse these very true distances AE, and the libration of Planet LE, of the crime of which my false method, which regarded I for F, was guilty.

Why many words?

Truth itself and Nature of things were rejected, and ordered to go into exile, by the back door they secretly received themselves back inside again, and were received by me under a foreign guise.

Leaving aside, I say, the librations of diameter LE, I began to recall ellipses, altogether believing that I was thus following a hypothesis far different from the librations.

They completely coincide, as will be demonstrated in the following chapter. By this reasoning, my sin in method was corrected, and F was used as it should have been.

My argument was as follows, as in Chapters 49, 50, and 56. The circle in Chapter 43 errs by excess, the ellipse in Chapter 45 errs by defect. That excess and this defect are equal. Between the circle and the ellipse there is nothing intermediate except another ellipse.

Therefore, the ellipse is the path of the planets. The crescent moon obtained by cutting away a semicircle has half the width of the former, namely 429.

If the path of the planets were an ellipse, it has been sufficiently shown that I cannot be used in place of F, because if this is done, the path of the planets becomes oval.

For let the angles GBD, HAK be equal below QBP, SAR.

Let the epicycle PT be drawn again with center R, equal to the former.

From P, by the intersection of the epicycle with the eccentric, let perpendiculars to BQ, AR, fall, PV, PM.

Let P be connected with B, and with center A, at distance AM, let the arc MN be drawn, cutting PV at O, PB at N.

Therefore, it is analogous to the above, that if we use I in place of F, then we now use N in place of O.

We can think that AN, as it is the right distance in length, is also right in position.

But the points I, N, and the like make the path of the planets oval. For the arcs GD and QP are equal.

BD, BP, drawn from a common center, cut the resected lunule.

But DI and PN, the widths of the lunule, extend towards the center and are unequal, and DI is smaller, PN is larger.

For since ED and MP are equal, and EDI, MPN are right angles, and El is a larger circle, as it has a longer radius AE, and MN is a smaller circle, as it has a shorter radius AM: PN will be altogether larger, DI smaller.

Therefore, the resected lunule is narrower above at D, wider below at P.

But in the ellipse this lunule is of equal width at points equally distant from the apsides G and Q. It is clear, therefore, that it is an oval path; therefore not an ellipse.

Since the ellipse provides correct equations, this oval path must provide incorrect ones.

There was no need to compute the equations from the ellipse all over again.

I knew they would do their job without a second thought. I was only concerned about the distances, lest perhaps those derived from the ellipse cause me trouble.

But even if this had happened, I had a hiding place ready, the uncertainty of 200 parts in the distances.

So I did not hesitate much here either.

But by far the greatest scruple was that, after considering and looking around almost to the point of madness, I could not find why the planet, to which, with such great probability and such a great consensus of observed distances, the libration LE in diameter LK was attributed, would rather go in an elliptical path, indicated by equations.

Oh, how ridiculous of me!

As if libration in diameter could not be the path to an ellipse.

Therefore, it cost me a great deal to learn this, that the ellipse is consistent with libration.

This will be clear in the following chapter where it will also be demonstrated that no other orbital figure is left for the planet, except a perfectly elliptical one. This is because of physical principles conspiring with the experience of observations and the vicarious hypothesis presented in this chapter.