Water Pressure
Table of Contents
I will tell you:
- how to separate the force of the vacuum from the others
- how to measure it
Water is a continuous substance whose parts allow separation except the separation from a void.
Whenever a cylinder of water is subjected to a pull. It offers a resistance to the separation of its parts because of the resistance of the void.
Let CABD be the cross section of a glass cylinder. Into this is introduced a perfectly fitting cylinder of wood, represented in cross section by EGHF, and capable of up-and-down motion.
Through the middle of this cylinder is bored a hole to receive an iron wire, carrying a hook at the end K, while the upper end of the wire, I, is provided with a conical head.
The wooden cylinder is countersunk at the top so as to receive, with a perfect fit, the conical head I of the wire, IK, when pulled down by the end K.
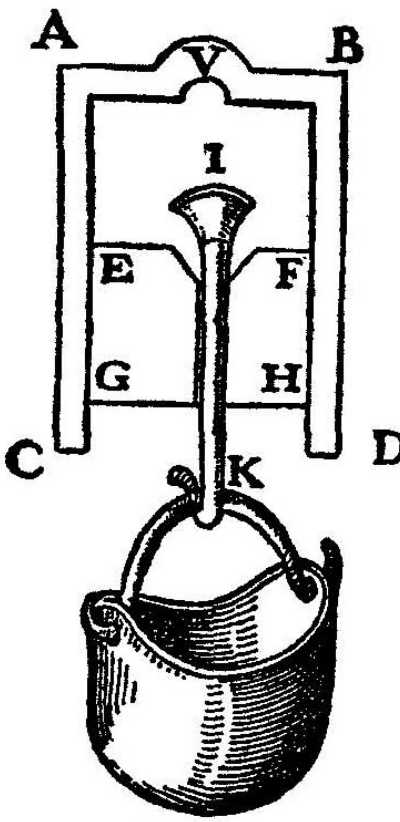
Insert the wooden cylinder EH in the hollow cylinder AD, so as not to touch the upper end of the latter but to leave free a space of 2 or 3 finger-breadths.
This space is to be filled with water by holding the vessel with the mouth CD upwards, pushing down on the stopper EH at the same time, keeping the conical head of the wire I away from the hollow portion of the wooden cylinder.
The air is thus allowed to escape alongside the iron wire (which does not make a close fit) as soon as one presses down on the wooden stopper.
The air was allowed to escape.
The iron wire was drawn back so that it fits snugly against the conical depression in the wood, invert the vessel, bringing it mouth downwards, and hang on the hook K a vessel which can be filled with sand or any heavy material in quantity sufficient to finally separate the upper surface of the stopper, EF, from the lower surface of the water to which it was attached only by the resistance of the vacuum.
Next, weigh the stopper and wire together with the attached vessel and its contents. We shall then have the force of the vacuum [forza del vacuo].
Attach to a glass cylinder a weight which, together with the weight of the marble or glass itself, is just equal to the sum of the weights before mentioned.
If breaking occurs, then the vacuum alone holds the parts of the glass together.
But if this weight does not suffice and if breaking occurs only after adding 4 times this weight, then the void furnishes only 1/5 of the total resistance.
I doubt its reliability. The air might creep in between the glass and stopper even if it is well packed with tow or other yielding material.
Will oiling with wax or turpentine be enoughy to make the cone I fit snugly on its seat?
Besides, the water might expand and dilate.
Why may not the air or exhalations or some other more subtile substances penetrate the pores of the wood, or even of the glass itself?
Water is by nature expansible, although only under severe treatment, we shall see the stopper descend.
If we put a small excavation in the upper part of the glass vessel, such as indicated by V, then the air or any other tenuous and gaseous substance, which might penetrate the pores of glass or wood, would pass through the water and collect in this receptacle V.
But if these things do not happen, our experiment has been performed with proper caution.
We shall discover that water does not dilate and that glass does not allow any material, however tenuous, to penetrate it.
I once saw a cistern which had been provided with a pump under the mistaken impression that the water might thus be drawn with less effort or in greater quantity than by means of the ordinary bucket.
The stock of the pump carried [64] its sucker and valve in the upper part so that the water was lifted by attraction and not by a push as is the case with pumps in which the sucker is placed lower down. This pump worked perfectly so long as the water in the cistern stood above a certain level.
But below this level the pump failed to work.
When I first noticed this phenomenon I thought the machine was out of order; but the workman whom I called in to repair it told me the defect was not in the pump but in the water which had fallen too low to be raised through such a height;
He added that it was not possible, either by a pump or by any other machine working on the principle of attraction, to lift water a hair’s breadth above 18 cubits; whether the pump be large or small this is the extreme limit of the lift. Up to this time I had been so thoughtless that, although I knew a rope, or rod of wood, or of iron, if sufficiently long, would break by its own weight when held by the upper end, it never occurred to me (17) that the same thing would happen, only much more easily, to a column of water. And really is not that thing which is attracted in the pump a column of water attached at the upper end and stretched more and more until finally a point is reached where it breaks, like a rope, on account of its excessive weight?
That is how it works.
This fixed elevation of eighteen cubits is true for any quantity of water whatever, be the pump large or small or even as fine as a straw. We may therefore say that, on weighing the water contained in a tube eighteen cubits long, no matter what the diameter, we shall obtain the value of the resistance of the vacuum in a cylinder of any solid material having a bore of this same diameter.
And having gone so far, let us see how easy it is to find to what length cylinders of metal, stone, wood, glass, etc. , of any diameter can be elongated without breaking by their own weight.
Take for instance a copper wire of any length and thickness; fix the upper end and to the other end attach a greater and greater load until finally the wire breaks.
Let the maximum load be, say, fifty pounds. Then it is clear that if fifty pounds of copper, in addition to the weight of the wire itself which may be, say, 1/8 ounce, is drawn out into wire of this same size we shall have the greatest length of this kind of wire which can sustain its own weight.
Suppose the wire which breaks to be one cubit in length and 1/8 ounce in weight; then since it supports 50 lbs. in addition to its own weight, i. e. , 4800 eighths-of-an ounce, it follows that all copper wires, independent of size, can sustain themselves up to a length of 4801 cubits and no more. Since then a copper rod can sustain its own weight up to a length of 4801 cubits it follows that that part of the breaking strength [resistenza] which depends upon the vacuum, comparing it with the remaining factors of resistance, is equal to the weight of a rod of water, eighteen cubits long and as thick as the copper rod.
If, for example, copper is nine times as heavy as water, the breaking strength [resistenza allo strapparsi] of any copper rod, in so far as it depends upon the vacuum, is equal to the weight of two cubits of this same rod.
By a similar method one can (18) find the maximum length of wire or rod of any material which will just sustain its own weight, and can at the same time discover the part which the vacuum plays in its breaking strength.