Simple Derivation Of The Lorentz Transformation

FOR the relative orientation of the coordinate systems K and K' below, the x-axes of both systems permanently coincide.

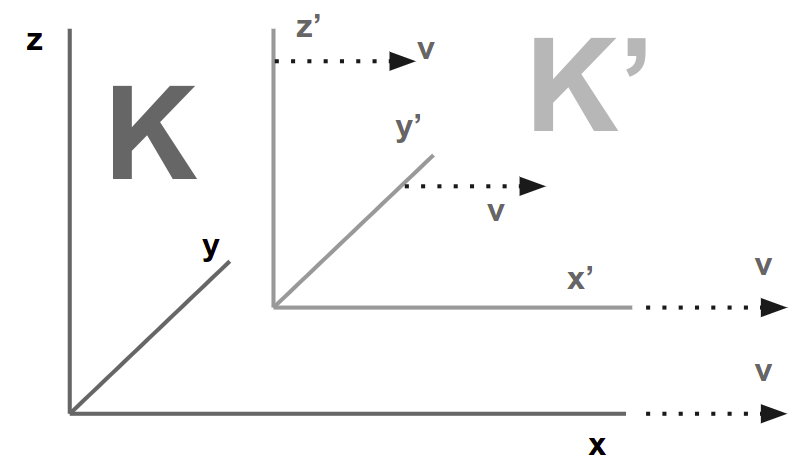
We can divide the problem into parts by considering first only events which are localised on the x-axis. Any such event is represented=

• with respect to the non-movingK by the abscissa x and the time t
• with respect to the moving K' by the abscissa x' and the time t'.

Find x' and t' when x and t are given.

A light-signal, moving along the positive axis of x, is transmitted according to the equation=

x − ct = 0 

Since the same light-signal has to be transmitted relative to the moving K' with the velocity c, the propagation relative to the moving K' will be represented by the analogous formula=

x' − ct' = 0

Those space-time points (events) which satisfy (1) must also satisfy (2). Obviously this will be the case when the relation

(x' − ct') = λ(x − ct)

is fulfilled in general, where λ indicates a constant; for, according to (3), the disappearance of (x − ct) involves the disappearance of (x' − ct').

If we apply quite similar considerations to light rays which are being transmitted along the negative x-axis, we obtain the condition=

(x' + ct') = µ (x + ct)

By adding (or subtracting) equations (3) and (4), and introducing for convenience the constants a and b in place of the constants λ and µ where

a = (λ + µ)/2
b = (λ − µ)/2 

we obtain the equations=

x' = ax − bct
ct' = act − bx 

We should thus have the solution of our problem, if the constants a and b were known. These result from the following discussion. For the origin of the moving K' we have permanently x' = 0. Hence, according to the first of the equations (5)

x = (bc/a)t

v is the velocity of the origin of the moving K' to the non-moving K. We then have=

v = bc/a

The same v can be obtained from equations * (5), if we calculate the velocity of another point of moving K' relative to non-moving K, or the velocity (directed towards the negative x-axis) of a point of non-moving K with respect to moving K'. In short, we can designate v as the relative velocity of the two systems.

Relativity says that= from the viewpoint of non-moving K, the length of a unit measuring-rod at rest in moving K' must be exactly as long as that of a unit measuring-rod at rest in non-moving K from the viewpoint from moving K'.

To see how the points of the x’-axis appear from the viewpoint non-moving K, we take a “snapshot” of moving K' from non-moving K. We have to insert a value of t (time of non-moving K), e.g. t = 0. For this value of t, we then obtain from the first of the equations (5) x' = ax.

Two points of the x’-axis which are separated by the distance ∆ x' = 1 when measured in moving K' are thus separated in our instantaneous photograph by the distance=

∆ x = 1/a

But if the snapshot were taken from moving K’ (t' = 0), and if we eliminate t from the equations (5), taking into account the expression (6), we obtain=

x' = a ( 1-(v2/c2) x

From this, we conclude that two points on the x-axis and separated by the distance 1 (relative to non-moving K) will be represented on our snapshot by the distance=

∆x' = a ( 1 − (v2/c2))

The two snapshots must be identical. Hence ∆x in (7) must be equal to ∆x’ in (7a), so that we obtain=

a2 = 1/ (1-(v2/c2))

The equations (6) and (7b) determine the constants a and b. By inserting the values of these constants in (5), we obtain the first and the fourth of the equations given in Section 11.

x' = (x-vt) / √ 1-(v2/c2)
t' = t - (v/c2) x / √ 1-(v2/c2)

Thus we have obtained the Lorentz transformation for events on the x-axis. It satisfies the condition

x'2 − c 2 t' 2 = x 2 − c 2 t 2

The extension of this result, to include events which take place outside the x-axis, is obtained by retaining equations (8) and supplementing them by the relations

y' = y
z' = z

In this way we satisfy the postulate of the constancy of the velocity of light in vacuo for rays of light of arbitrary direction, both for the system K and for the system K’. This may be shown in the following manner.

A light-signal is sent out from the origin of non-moving K at the time t = 0. It will be propagated according to the equation=

r = x 2 + y 2 + z 2 = ct

or, if we square this equation, then=

x 2 + y 2 + z 2 − c 2 t 2 = 0

It is required by the law of propagation of light, in conjunction with the postulate of relativity, that the transmission of the signal in question should take place — as judged from K’ — in accordance with the corresponding formula=

r' = ct'
or
x' 2 + y' 2 + z' 2 − c 2 t' 2 = 0

In order that equation (10a) may be a consequence of equation (10), we must have=

x'2 + y'2 + z'2 − c2 t'2 = σ ( x2 + y2 + z2 − c2 t2 )

Since equation (8a) must hold for points on the x-axis, we thus have σ = 1. We see that the Lorentz transformation really satisfies equation (11) for σ = 1; for (11) is a consequence of (8a) and (9), and hence also of (8) and (9).

We have thus derived the Lorentz transformation.

The Lorentz transformation represented by (8) and (9) still requires to be generalised. It is not essential=

• whether the axes of moving K' be chosen so that they are spatially parallel to those of non-moving K
• that the velocity of translation of moving K’ with respect to non-moving K should be in the direction of the x-axis.

We can construct the Lorentz transformation in this general sense from two kinds of transformations=

• from Lorentz transformations in the special sense
• from purely spatial transformations, which corresponds to the replacement of the rectangular co-ordinate system by a new system with its axes pointing in other directions.

Mathematically, we can characterise the generalised Lorentz transformation thus=

It expresses x', y', z', t', in terms of linear homogeneous functions of x, y, z, t, of such a kind that the relation=

x'2 + y'2 + z'2 − c2 t'2 = x2 + y2 + z2 − c2 t2

is satisfied identically. That is to say= If we substitute their expressions in x, y, z, t, in place of x’, y’, z’, t’, on the left-hand side, then the left-hand side of (11a) agrees with the right-hand side.