Refraction Angles

Let us assume that the ball was pushed from A to B.

While at point B, it is pushed further by the racket CBE.

This increases the force of its movement by 1/3 so that it can cover as much distance in 2 moments as it did in 3 moments before.

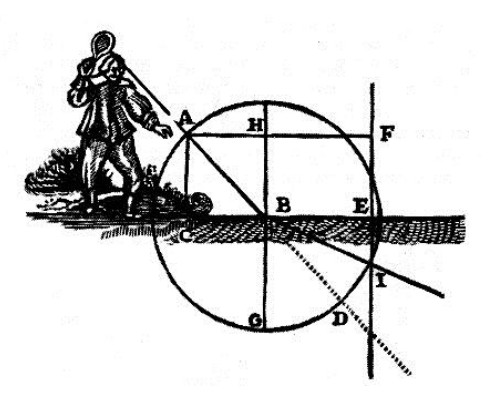
This will have the same effect as if it encountered at point B a body of such nature that it passed through its surface CBE, a third more easily than through the air.

Draw circle AD and the lines AC, RB, FE, in a way that there is 1/3 less distance between FE and RB than between RB and AC.

The straight line FE and the circular AD intersect at the point I.

• This will designate where this ball, being at point B, must deflect.

The reverse of this conclusion is as follows.

The ball that comes from A in a straight line to B deflects at point B.

• From there, it goes to I.
• This means that its force to enter the body CBEI is proportional to the force it exits the body ACBE, as the distance between AC and HB is to the distance between HB and FI, that is, as the line CB is to BE.

The action of light follows the same laws as the motion of this ball.

When its rays pass obliquely from one transparent body to another, which receives them more or less easily than the first, they are deflected in such a way that they are always less inclined towards the surface of these bodies on the side where they are received most easily, than on the side where the other is located.

This, just in proportion to how much more easily they are received by the one than by the other.

This inclination should be measured by the quantity of straight lines, such as CB or AH, and EB or IG, and similar ones, compared to each other.

It should not be measured by the angle of the lines, such as ABH or GBI, nor by the angle of the semblables to DBI, which are called the angles of refraction.

This is because the proportion that exists between these angles varies with all the different inclinations of the rays; whereas the proportion that exists between the lines AH and IG, or similar ones, remains the same in all the refractions caused by the same bodies.

For example, if a ray passes from A to B in the air, and, encountering the surface of the glass CBR at point B, is deflected towards I within the glass; and another ray passes from K to B, which is deflected towards L; and another from P to R, which is deflected towards S; then the proportion between the lines KM and LN, or PQ and ST, should be the same as between AH and IG, but not the same as the proportion between the angles KBM and LBN, or PRQ and SRT, and the angle ABH and IBG.

• Since AH = CB and EB = IG, the ratio CB/BE is equivalent to the ratio of the sines (AH/AB and IG/BI, or AB and IB being equal to the unit ray, AH and IG) of the angle of incidence ABH and the angle of refraction GBI. The law of refraction expresses the constancy of the ratio of the two sines, as a function of the index of refraction (n) of the two media considered, that is: AH = n . IG.