Water Droplets

by Rene Descartes Icon

4 minutes • 711 words

Let AFD be a drop of water.

Its half diameter CD or AB is divided into as many equal parts as needed to calculate rays that will attribute as much light to some as to others.

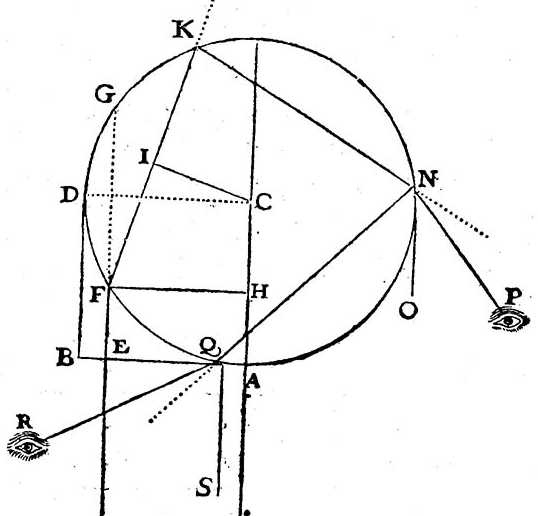
Take ray EF.

Instead of going straight towards G, it turns towards K and reflects from K towards N.
From N it goes towards the eye P

Or reflect it from N towards Q.

From there turn towards the eye R.

Draw CI at right angles to FK.

AE or HF and CI have between them the proportion that measures the refraction of water.

If HF contains 8,000 parts, then:

AB contains 10,000
CI will contain around 5,984

This is because the Refraction of water is slightly greater than 3:4, more like 187:250.

From the lines HF and CI, I easily know the 2 arcs:

FG is 73 degrees and 44 minutes
FK is 106. 30.

Remove twice the arc FK from the arc FG added to 180 degrees. This leaves 40. 44. for the quantity of the angle ONP because I suppose ON parallel to EF.

Removing these 40. 44 from FK, I have 65. 46 for the angle SQR. This is because I also pose SQ parallel to EF.

We calculate in the same way all the other rays parallel to EF, which pass through the divisions of the diameter AB:

HF	CI	FG	FK	ONP	SQR
1,000	7,481	168.30	171.25	5.40	165.45
2,000	1,496	156.55	162.48	11.19	151.29
3,000	2,244	145.40	154.4	17.56	136.8
4,000	2,992	132.50	145.10	22.30	122.4
5,000	3,740	120.00	136.4	27.52	108.12
6,000	4,488	106.16	126.4	32.56	93.44
7,000	5,236	91.8	116.51	37.26	79.25
8,000	5,984	73.44	106.3	40.44	65.46
9,000	6,732	51.41	95.22	40.57	54.25
10,000	7,480	0	83.10	13.40	69.30

In this table that there are many more rays that make the angle ONP of about 40 degrees, than there are that make it less; or SQR of about 54, than there are that make it greater.

Then in order to make it even more precise I do this table:

Line HF	Line CI	Arc FG	Arc FK	Angle ONP	Angle SQR
8000	5984	73.44	106.30	40.44	55.46
8100	6058	71.48	105.25	40.58	64.37
8200	6133	69.50	104.20	41.10	53.10
8300	6208	67.48	103.14	41.20	52.54
8400	6283	65.44	102.9	41.26	61.43
8500	6358	63.34	101.2	41.30	60.32
8600	6432	61.22	99.56	41.30	38.26
8700	6507	59.4	98.48	41.28	57.20
8800	6582	56.42	97.40	41.22	56.18
8900	6657	54.16	96.32	41.12	55.20
9000	6732	51.41	95.22	40.57	54.25
9100	6806	49	94.12	40.36	53.35
9200	6881	46.8	93.2	40.45	52.58
9300	6956	43.8	91.51	39.26	52.25
9400	7031	39.54	90.38	38.38	52.37
9500	7106	36.24	89.26	37.32	51.54
9600	7180	32.30	88.12	36.6	65.24
9700	7255	28.8	87	34.12	52.40
9800	7330	22.57	85.43	31.31	54.12

I see here that the largest angle ONP can be 41 degrees 30 minutes.

The smallest SQR is 51.54, to which adding or subtracting about 17 minutes for the half diameter of the sun, I have 41.47 for the largest half diameter of the inner rainbow, and 51.37 for the smallest of the outer one.

When water is hot, its refraction is slightly less than when it is cold, which can change something in this calculation.

However, this cannot increase the half diameter of the inner rainbow by more than one or two degrees at most. And then, that of the outer one will be almost twice as small.

This demonstrates that the refraction of water cannot be much less or greater than I suppose.

If it were only a little greater, it would make the half diameter of the inner rainbow less than 41 degrees, instead of which, by common belief, it is given 45 degrees.

If we suppose it small enough to make it really 45, we will find that that of the outer one will not be much more than 45 either, instead of which it appears to the eye to be much larger than that of the inner one.

Maurolycus was the first to have determined one of 45 degrees. He determines the other to be about 56.

This shows the little faith that should be added to observations that are not accompanied by true reason.